Was ist eine Exponentialfunktion?
gedruckt am 22. Jan. 2025
Exponentielle Zusammenhänge sind jene Zusammenhänge, die für gleiche absolute Änderungen der einen Größe (x) gleiche prozentuelle (nicht absolute) Änderungen der anderen Größe (y) ergeben. Der Prozentsatz wird dabei vom jeweils aktuellen x-Wert berechnet und ist konstant.
Ein Auto verliert pro Jahr 30% seines aktuellen Wertes. Ermittle eine Tabelle für den jeweiligen Wert eines Wagens, der neu 20.000 EUR kostet. Berechne den Wert bis zum zehnten Jahr und zeichne die berechneten Werte in ein Koordinatensystem.
Der Term dieser Exponentialfunktion heißt
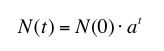
In diesem Fall gilt: N(0) = 20.000 und a = 0,7 (weil nach einem Jahr der Wert auf 70% des vorigen Wertes sinkt). N(t) ist der Wert nach t Jahren.
Der mathematische Gehalt von Berechnungen exponentieller Zusammenhänge ist die Potenzrechnung mit ihren Umkehrungen Radizieren und Logarithmieren. Bei Fragestellungen mit unbekanntem Exponenten ist für die Berechnung die Rechenart Logarithmus nötig. (Siehe Kapitel Logarithmus)
Da der aktuelle Bestand bei exponentiellen Zusammenhängen eine Rolle spielt (zum Berechnen der Prozente), spricht man auch von Wachstum mit Rückkoppelung. Lineares Wachstum ist Wachstum ohne Rückkoppelung, der aktuelle Bestand spielt bei linearen Zusammenhängen keine Rolle für die Größe des Zuwachses, der ist immer (absolut) gleich groß.
2. Platz für eContent für eLearning in der Kategorie Sekundarstufe II am 10.11.2014 in Wien gemeinsam mit Mag. Hannes Mitterlehner (Mitte) für das Projekt 
Mai 18th, 2011 at 20:53
Hallo Christian!
Nach 1 Jahr sind es 14.000, das stimmt. Gerechnet: 20.000*0,70 = 14.000, das sind 70%.
Das 2. Jahr wird mit 70% vom ersten Jahr berechnet: 14.000*0,7 = 9.800 oder 20.000*0,7*0,7 = 20.000*0,7^2 (0,7 zum Quadrat).
Und geht das dann weiter. Voriges Jahr * 0,7 oder Anfangswert*0,7 hoch Jahre.
Alles klar?