jomo.org

Themenbereiche der Rentenrechnung sind unter anderem: gleichmäßiges Ansparen (etwa private Pensionsversicherung), gleichmäßige Auszahlungen (Privatpensionsgenuss), Kreditrückzahlungen, Ratenkäufe.

Die finanzmathematischen Grundbegriffe sind: Rentendauer bzw. Rentenlaufzeit, Rentenperiode, Periodenzinssatz, Rate, Barwert und Endwert. Zu unterscheiden ist, ob die einzelnen Raten am Ende oder am Anfang einer Periode fällig sind: Wird am Ende einer Periode ein- oder ausgezahlt, so nennt man die Rente nachschüssig, bei Fälligkeit am Beginn einer Periode heißt die Rente vorschüssig. Vorschüssigkeit oder Nachschüssigkeit einer Rente hängt vom Thema bzw. Zusammenhang ab und steht zumindest indirekt im Vertrag: Eine Kreditrückzahlung wird eher nachschüssig sein, weil ich mit Erhalt des Kreditbetrages nicht gleich wieder einen Teil als Rate abgeben werde. Versicherungssparen wird vorschüssig sein, weil ich mit Vertragsbeginn zahlen werden und erst am Ende der Periode der letzten Einzahlung über den Betrag als Endwert verfügen werde.

Der Barwert ist der Wert aller Zahlungen bezogen auf den Beginn der Rente. Da bei einer vorschüssigen Rente alle Zahlungen genau eine Periode länger verzinst werden als bei einer nachschüssigen Rente, entspricht der Barwert einer vorschüssigen Rente dem um eine Periode aufgezinsten Barwert einer nachschüssigen Rente.

Der Endwert einer Rente ist der Wert aller Zahlungen bezogen auf das Ende der Rente. Der Endwert ist daher der über die gesamte Rentendauer (Anzahl der Perioden) aufgezinste Barwert (vor- oder nachschüssig).

Als Zinssatz wird in der Rentenformel der äquivalente Periodenzinssatz verwendet. Bei einer Monatsrente ist das der Monatszinssatz.

Als Rentenformel empfehle ich die nachschüssige Barwertformel zu kennen und alle anderen Varianten aus dieser herzuleiten:

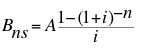
wobei
B_ns … Barwert einer nachschüssigen Rente,
A … Rate,
i … Periodenzinssatz,
n … Anzahl der Rentenperioden

B_vs = B_ns(1+i)
E_ns = B_ns(1+i)ⁿ
E_vs = B_vs(1+i)ⁿ = B_ns(1+i)ⁿ⁺¹

Die nachschüssige Barwertformel kann einfacher hergeleitet werden als in der traditionellen mathematischen Unterrichtsliteratur üblich:

Im Falle sich ändernder Zinssätze müssten für Teilrenten die Bar- oder Endwerte berechnet werden und diese dann entsprechend ihrer zeitlichen Lage entsprechend auf- oder abgezinst werden, um die einzelnen Teilbeträge dann addieren zu können. Auf einzelne ausbleibende Zahlungen (Kreditrückzahlung) muss ebenfalls entsprechend durch Rentenkonvertierung reagiert werden. Derartige Rechenübungen halte ich allerdings im Unterricht nicht für sinnvoll, da sie vom Grundverständnis zu sehr ablenken.