Eine Flüssigkeit kühlt ab
gedruckt am 31. Jan. 2026
Die Abkühlung von Temperaturen kann als exponentielles Modell beschrieben werden. Zu beachten ist allerdings, daß Temperaturen nicht auf 0° abkühlen, sondern auf die Umgebungstemperatur. Im Abkühlungsmodell muss also die Umgebungstemperatur berücksichtigt werden:
Man stelle sich das anhand konkreter Daten vor:
Die Anfangstemperatur To ist 90°C, die Umgebungstemperatur Tu ist 20°C.
Nach 2,5 Minuten sei eine Flüssigkeit auf T(2,5) = 60°C abgekühlt.
Nun entspricht der Abkühlungsvorgang einer Abkühlung von 70°C ( T(0) – Tu ) auf 0°C
mit T(2,5) = 40°C (T(2,5) – Tu) auf folgende Weise:
T(t) – Tu = (T(0) – Tu) at . . . von T(t) und T(0) wird Tu subtrahiert
bzw.
T(t) = (To – Tu) at + Tu . . . explizierte Darstellung
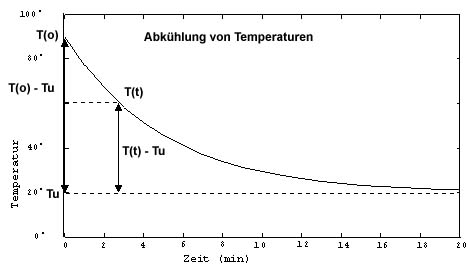
Graphisch entspricht dieser Berücksichtigung der Umgebungstemperatur eine Parallelverschiebung der Exponentialfunktion entlang der y-Achse bzw. einer Parallelverschiebung der x-Achse. Man denkt sich die x-Achse in der Höhe der Umgebungstemperatur und passt die Formel entsprechend an: statt Tu schreibt man Tu – To und statt T(t) schreibt man T(t) – To.


 2. Platz für eContent für eLearning in der Kategorie Sekundarstufe II am 10.11.2014 in Wien gemeinsam mit Mag. Hannes Mitterlehner (Mitte) für das Projekt
2. Platz für eContent für eLearning in der Kategorie Sekundarstufe II am 10.11.2014 in Wien gemeinsam mit Mag. Hannes Mitterlehner (Mitte) für das Projekt 