Die Logik der Gaußschen Zahlenebene für komplexe Zahlen
gedruckt am 08. Mar. 2026
Ausgehend von der Zahlengeraden kann man die Grundrechnungsarten als Operationen mit Pfeilen interpretieren: Pfeile werden addiert, subtrahiert, gestreckt und gestaucht, und um 180° in die entgegengesetzte Richtung gerichtet (Multiplikation einer Zahl mit -1).
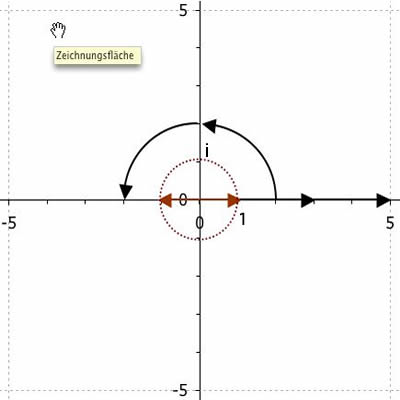
Die Entstehung der komplexen Zahlenebene
Bei Mehrfachmultiplikation mit -1 wird der Pfeil zweimal gegen den Uhrzeigersinn gedreht. Die ganzzahligen Potenzen von -1 als Drehung um jeweils 1mal, 2mal, etc um 180° Drehung nach links. Die Wurzel aus -1 könnte in Analogie als halbe Drehung ((-1)1/2, also um Drehung um nur 90° interpretiert werden. Diese sinnvolle und (ana)logische Erweiterung dieses Operatoren-Konzeptes führt aus der Zahlengerade hinaus in die Zahlebene. Den Zielpunkt der Operation Wurzel(-1) nennt man i (imaginäre Einheit), bei Wurzel(-2) steht dann 2i, etc. Auf diese Weise entsteht die imaginäre Zahlenachse in Ergänzung zur reellen Zahlenachse (der üblichen Zahlengeraden).
Zahlen in der Ebene, die duch die beiden Achsen aufgespannt wird, heißen komplexe Zahlen, sind also zusammengesetzte Zahlen.
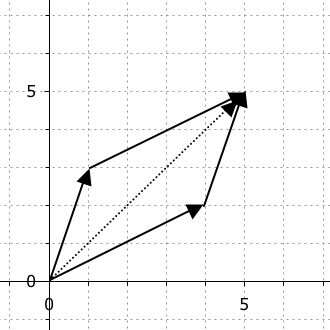
Addition zweier komplexer Zahlen
Rechnen mit komplexen Zahlen kann ebenfalls als Operation mit Pfeilen gedeutet werden: Pfeile in unterschiedlicher Länge in unterschiedliche Richtungen werden entsprechend gerichtet aneinandergefügt, das Ergebnis ist der Pfeil vom Koordinatenursprung zum Zielpunkt.
Die komplexen Zahlen können verschieden notiert werden, je nachdem, in welchem Zusammenhang man sie sieht bzw. verwendet:
Die Schreibweise 4+2i deutet noch auf die Herkunft der Wurzel aus einer negativen Zahl hin, die Schreibweise (4, 2) deutet auf die Verwendung im geometrischen Kontext hin.
Anwendungen wie die Kräftephysik mit dem Kräfteparallelogramm zeigen, dass diese Zahlenerweiterung nicht nur geometrisch, sondern auch inhaltlich Sinn macht. Rechnen mit 2-dim-Vektoren kann als Rechnen mit komplexen Zahlen interpretiert werden.
Einige Konsequenzen und Fragestellungen
Imaginäre bzw. Komplexe Zahlen sind weder positiv noch negativ, weil sie nicht auf der Zahlengeraden liegen.
Der Größenvergleich komplexer Zahlen muss neu definiert werden: Jene komplexe Zahl ist größer als eine andere, deren Abstand zum Koordinatenursprung (das nennt man Betrag der Zahl z) größer ist.
Überlege:
- Wie kann man komplexe Zahlen multiplizieren, wie potenzieren? Kann auch der Exponent in einer Potenz eine komplexe Zahl sein? Ist das Ergebnis der Rechnung mit komplexen Zahl immer eine komplexe Zahl oder müssen wir den Zahlenbereich immer wieder erweitern?
Überlege:
- Wie verändert sich Funktionsbegriff, wenn als Grundmenge für die x-Werte nicht die Zahlengerade, sondern die komplexe Zahlebene verwendet wird? (Stichwort: komplexen Funktionentheorie).
- Wie sollen wir solche komplexen Funktionen zeichnen?


 2. Platz für eContent für eLearning in der Kategorie Sekundarstufe II am 10.11.2014 in Wien gemeinsam mit Mag. Hannes Mitterlehner (Mitte) für das Projekt
2. Platz für eContent für eLearning in der Kategorie Sekundarstufe II am 10.11.2014 in Wien gemeinsam mit Mag. Hannes Mitterlehner (Mitte) für das Projekt 