jomo.org

Übung zum Problembewußtsein: Stelle die Exponentialfunktion zur Basis 10 grafisch dar (Bereich für die x-Werte: 0 bis 5) und versuche, im Bereich zwischen x = 0 und 2 Unterschiede der y-Werte festzustellen!

Um dieses Problem zu umgehen, wird die y-Skala logarithmisch skaliert, das heißt anstelle von 0, 1, 2, … wird in gleichen Abständen 10hoch0, 10hoch1, 10hoch2, geschrieben. Der Verlauf der Kurve wird dadurch verzerrt, die y-Werte werden in allen Bereichen leichter vergleichbar. Interessanterweise wird der Graf dieser Exponentialfunktion zu einer Linie bzw. Geraden mit der Steigung 1.

Um beliebige Exponentialfunktionen linear darstellen zu können (damit in allen Größenbereichen Unterscheidungen zu sehen sind), muss die Exponentialfunktion zur Basis 10 dargestellt werden:

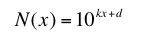
Die Umformung geschieht wie folgt:

Achtung: Die mögliche logarithmische Skalierung der y-Achse hat eine wichtige Konsequenz: nicht alles, was aussieht wie eine Gerade ist auch eine Gerade! Zu allererst muss man die y-Achse beachten, um die Entscheidung treffen zu können: Lineare Funktion oder Exponentialfunktion.

Hinweis: Es kann auch die x-Achse logarithmisch skaliert werden. In diesem Fall werden Logarithmus-Funktionen linear dargestellt. Werden x-Achse und y-Achse beide logarithmisch skaliert, so werden Potenzfunktionen linear dargestellt.

Beispiele

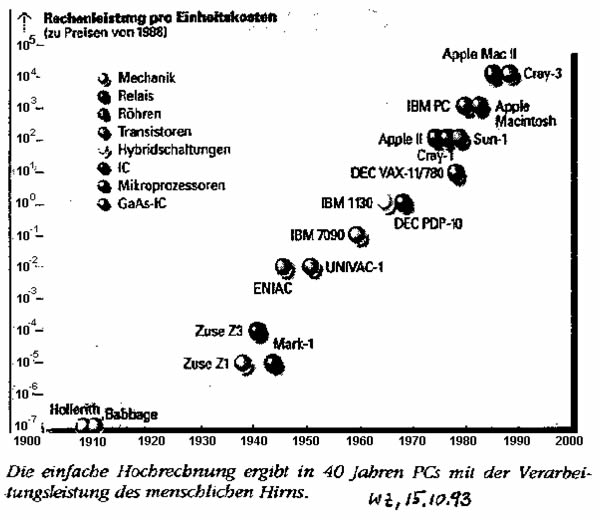
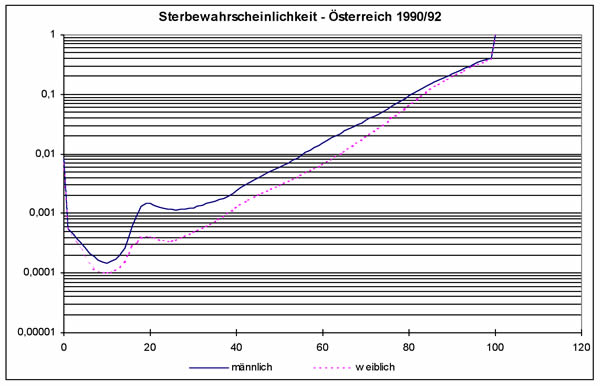
1. Erkläre, was diese Funktionen darstellen!
2. Warum ist in diesen Abbildungen die y-Achse logarithmisch skaliert?
3. Ermittle unter Verwendung mehrerer repräsentativer Datenpunkte die entsprechende Funktion und deute die erhaltenen Parameter! (Hinweis: Rechne bei den Sterberaten nur ab 30jährige!)
4. Stelle die erhaltenen Funktionsterme auch zur Basis a dar!
5. Stelle einzelne der bereits bekannten Themen und Beispiele (radioaktiver Zerfall, Lichtintensität, …) zur Basis 10 dar und zeichne die Funktion mit logarithmisch skalierter y-Achse!