Die Grundidee der Differentialrechnung
gedruckt am 24. Apr. 2018
Anmerkung zum Funktionsbegriff: Eine Funktion zeigt den Zusammenhang zweier Größen, indem die eine als abhängig von der anderen gedacht wird. Diese Abhängigkeit ist formal und wird durch eine Formel ausgedrückt, den Funktionsterm. Die abhängige Größe wird meist mit y oder f(x) bezeichnet, die andere Größe x. Der Funktionsterm gibt jene Formel an, mit der man die abhängige Größe f(x) aus einem x berechnen kann. Alle möglichen Werte von f(x) grafisch dargestellt zeigen den Funktionsverlauf oder Funktionsgraf.
Gemessen wird der Grad der Veränderung mit Hilfe der Steigung der Tangente an einer bestimmten Stelle der Funktion xo. Steigt die Funktion in einem Bereich stärker/schwächer, ist die Tangentensteigung dort größer/kleiner. Fällt eine Funktion (gelesen von inks nach rechts), dann sind die Tangentensteigungen negativ.
Wir könnten jetzt für jeden Punkt einer Funktion die Tangentensteigung ermitteln: Die einzelnen Tangentensteigungen zeichnen wir in das Diagramm, sie liegen auf einer Funktion, der Tangentensteigungsfunktion. Diese Funktion nennt man 1. Ableitung von f(x): f'(x). Die 1. Ableitung repräsentiert also die Tangentensteigungen von f(x) in jedem Punkt.
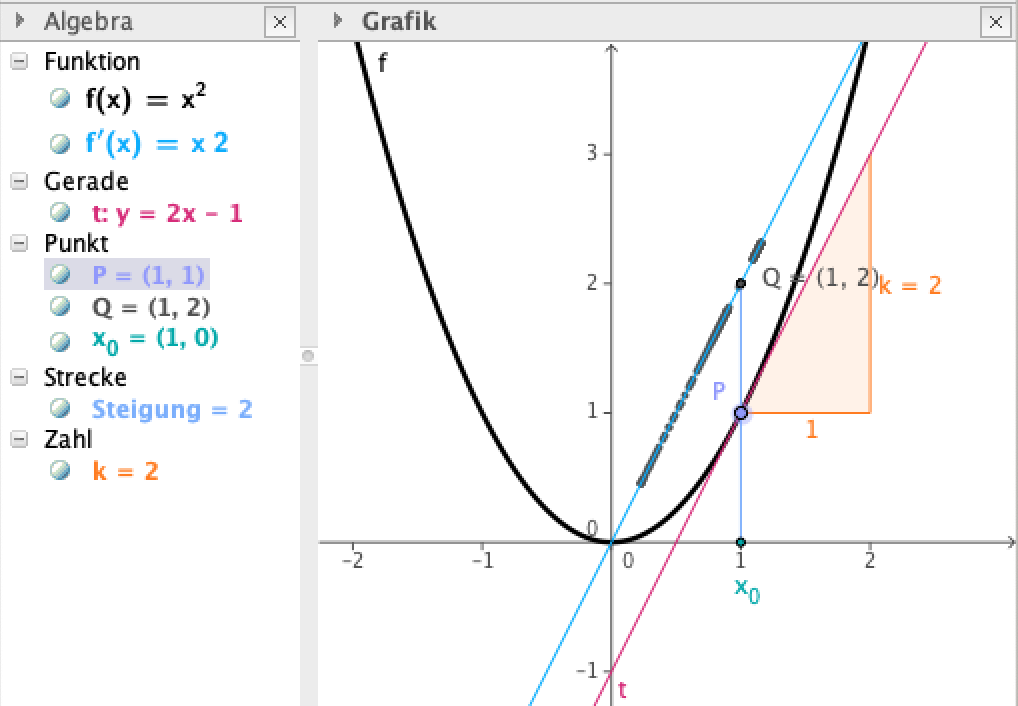
Die erste Ableitung als Tangentensteigungsfunktion
Kommentar zur Abbildung
- An der Stelle x=1 wird im Punkt A auf der Funktion die Tangente an die Funktion f (rot) gebildet, diese hat die Steigung -1.35.
- Dieser Wert wird an der x-Stelle 1 als y-Wert einer neuen Funktion, der Tangentensteigungsfunktion bzw. ersten Ableitung von f, aufgetragen (Punkt B).
- Ermittelt man jetzt mehrere solcher Tangentensteigungen für andere x-Stellen, so liegen die Steigungen auf der ersten Ableitung (blau).
2. Platz für eContent für eLearning in der Kategorie Sekundarstufe II am 10.11.2014 in Wien gemeinsam mit Mag. Hannes Mitterlehner (Mitte) für das Projekt 