Wählerstromanalysen 3: Übungsbeispiele
gedruckt am 06. Feb. 2026
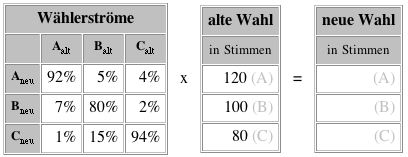
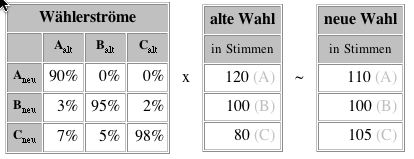
Hinweis: A, B, C sind drei politische Parteien. Das Matrixelement a12 = 5% (= 0,05) bedeutet, dass 5% der ehemaligen Wähler von B diesmal A wählen. Die Wahlergebnisse sind bei diesen Aufgaben in Stimmen gegeben, können aber auch in Prozent der Wähler gesetzt werden.
a. Interpretiere die einzelnen Prozentsätze der Wählerstrommatrix!
b. Berechne die prognostizierten Stimmen für die neue Wahl!
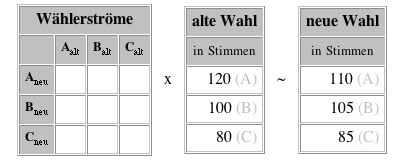
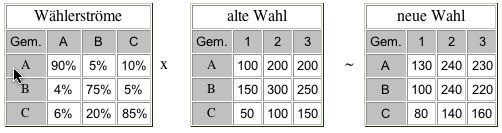
2. a. Versuche mit Hilfe gezielten Probierens, aus den beiden Ergebnissen zweier aufeinanderfolgender Wahlen die Wählerstrommatrix zu ermitteln! Begründe, für welche Ausgangsmatrix du dich entscheidest.
b. Versuche weiters, für die gleichen Daten eine andere Matrix zu finden um zu zeigen, daß die Ermittlung der Matrix (bei einem einzigen Wahlergebnis) nicht eindeutig ist!
c. Das Probieren geht mit Hilfe eines EXCEL-Arbeitsblattes schneller. Erstelle ein Modell für diese Matrizenmultiplikation in EXCEL! Hinweis: Die Zeile „Cneu“ soll mit Hilfe einer Formel (Spaltensumme = 1) berechnet werden, Dateneingabe also nur in den Zeilen „Aneu“ und „Bneu„.
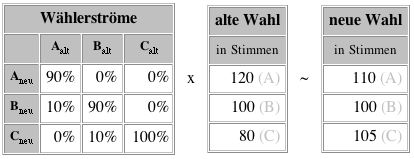
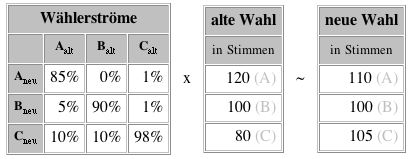
3. Bei den folgenden Matrizen ist die Summe der Stimmen bei zwei aufeinanderfolgenden Wahlen ungleich groß. Die Matrizenmultiplikation kann daher nur eine Näherung an das neue Wahlergebnis bringen.
a. Berechne die prognostizierten Stimmen und vergleiche sie mit dem angegebenen Wahlergebnis!
b. Welche dieser drei Wählerstrommatrizen nähert das Verhalten der Wähler deiner Meinung nach am besten an? Begründe deine Entscheidung!
4. In den obigen Bespielen sind die Wählerströme in Prozent der Wähler gegeben.
a. Stelle die Wählerströme der obigen Beispiele auch in Anzahlen von Stimmen dar!
b. Stelle die Wählerströme in Stimmen als Balken- oder Säulendiagramm dar!
c. Erfinde ein Beispiel mit zwei größeren und einer kleinen Partei und stelle die Wählerströme auch in Stimmen dar. Was fällt dir auf?
5. Erstelle ein EXCEL-Modell, das für die Wahlergebnisse in drei Wahlsprengeln eine gemeinsame Wählerstrommatrix zugrundelegt! Multipliziere die Wählerstrommatrix mit den Stimmen der alten Wahl für jeden Wahlsprengel (1, 2, 3) und berechne die Abweichungen dieser Prognosen (Summe der Differenzen der Quadrate) vom tatsächlichen Ergebnis (Matrix „neue Wahl“ für drei Sprengel).
Kannst du eine bessere Wählerstrommatrix finden?
6. a. Erstelle die Struktur einer Tabelle für Wählerstromanalysen mit fünf Parteien!
b. Berücksichtige auch Nichtwähler und Ungültigwähler!
c. Wie könntest du die Tabelle organisieren, um auch Aufschlüsse über Jungwähler zu erhalten?
7. Wir haben festgestellt, daß Wählerstromanalysen das Wählerverhalten nur näherungsweise wiedergeben. Nenne einige Probleme der Berechnung und formuliere die nötigen Vereinfachungen! Erwähne zumindest drei Problembereiche!
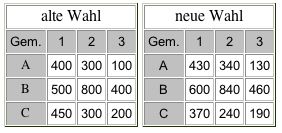
8. In drei Gemeinden (1 – 3) treten die drei Parteien A, B und C zur Wahl an. Die Ergebnisse der alten und der neuen Wahl können den nachstehenden Tabellen entnommen werden.
a. Ermittle eine Wählerstrommatrix, die für alle drei Gemeinden gut paßt!
b. Berechne die Summe der Quadrate der Differenzen zwischen Prognose (Matrizenmultiplikation) und angegebenen Ergebnissen!
c. Stelle die Wählerströme graphisch dar (Säulen- oder Balkendiagramm)!
9. Erstelle ein Wählerstromanalyse-Modell für EXCEL (notfalls nur auf Papier mit den Formeln) und versuche ausgehend von deinen (politischen) Annahmen die Wählerstrommatrix 1991-1997 zu finden!
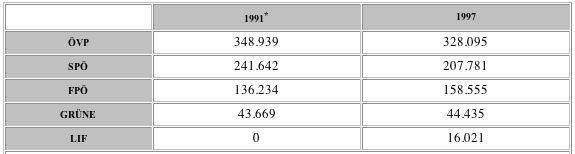
* Aus den Prozentsätzen 1991 und den Stimmen 1997 berechnet! Mit Hilfe dieser Vereinfachung (gleiche wahlwerbende Parteien und Stimmenanzahl) läßt sich einfacher eine Wählerstrommatrix finden.
Als Datengrundlage dienen die Gesamtergebnisse der Landtagswahlen 1991* und 1997 (einfaches Modell):
10.a. Erkläre jemandem (Familie, Freundeskreis), was Wählerstromanalysen sind, wie und warum sie gemacht werden! Halte deine Erklärung und die Verstehensprobleme deines Gesprächspartners in Stichworten fest!
b. Fasse das wichtigste über Wählerstromanalysen mit Beispielen übersichtlich zusammen!
11. Für politisch besonders Interessierte: Besorge dir die Ergebnisse der letzten beiden Gemeinderatswahlen (nach Wahlsprengel). Die Ergebnisse sind bei den Gemeindeämtern zu erhalten. Erstelle mit den Daten ein Modell für eine Wählerstromanalyse und führe die Analyse (SOLVER) durch. Überprüfe, ob die Ergebnisse auch politisch plausibel sind.


 2. Platz für eContent für eLearning in der Kategorie Sekundarstufe II am 10.11.2014 in Wien gemeinsam mit Mag. Hannes Mitterlehner (Mitte) für das Projekt
2. Platz für eContent für eLearning in der Kategorie Sekundarstufe II am 10.11.2014 in Wien gemeinsam mit Mag. Hannes Mitterlehner (Mitte) für das Projekt 