Taylorreihen und Taylorpolynome
gedruckt am 25. Dec. 2025
In diesem Kapitel geht es um das Auffinden von einfachen Näherungsfunktionen für komplizierte Funktionen. Unter einfachen Funktionen versteht man hier Potenzfunktionen beliebig hoher Ordnung, komplizierte Funktionen sind hier in erster Linie die Winkelfunktionen, die Exponential- und Logarithmusfunktionen. Man kann aber auch Potenzfunktionen höherer Ordnung durch Potenzfunktionen niedriger Ordnung annähern.
Die Näherungsfunktionen sind nur in einem bestimmten Bereich eine gute Näherung.Die Grundidee ist, dass man die Funktion an einer bestimmten Stelle a betrachtet und durch ihre Näherung ersetzt. An der Stelle x = a wird die Funktion einfach durch ihren Funktionswert ersetzt.
Möchte man den Trend der Funktion an der Stelle x = a zur Näherung hinzufügen, so wird die Tangente an die Funktion an dieser Stelle berechnet.
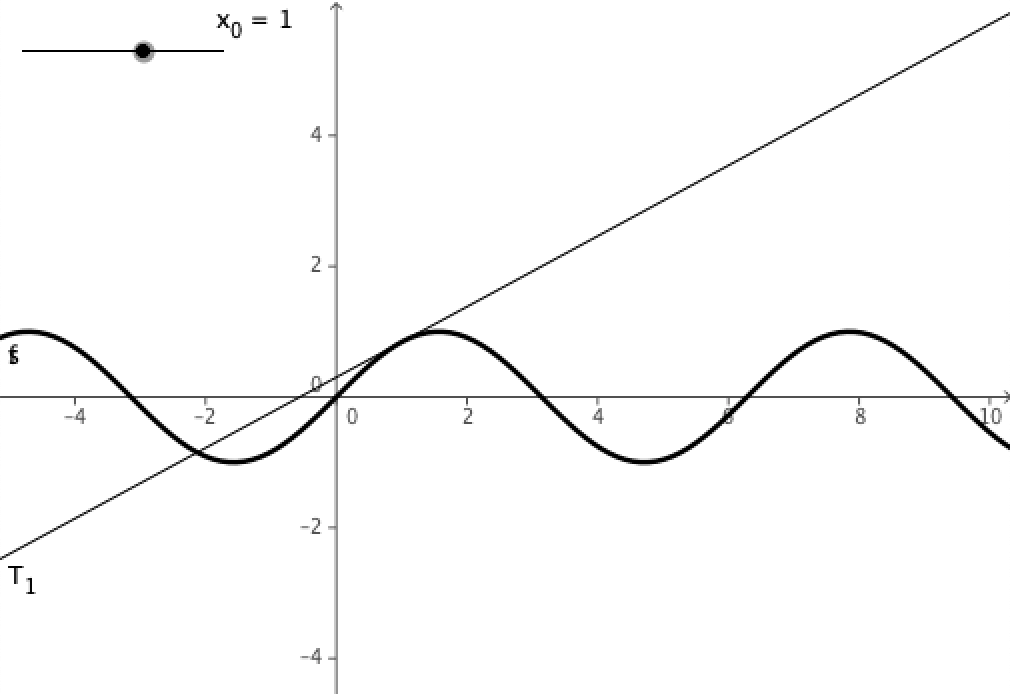
T1(x) nennt man auch Linearisierung von f an der Stelle xo=a. Die Linearisierung ist natürlich nur in einem engen Intervall um a als Trend sinnvoll. Der Gleichungsterm entspricht umgeformt dem linearen Funktionsterm T1(x) = f(xo) + f'(xo).(x – xo). Die Tangentengleichung als lineare Näherungsfunktion für f(x) an der Stelle xo=a.
Möchte man zum linearen Trend auch das Krümmungsverhalten bei x = a einbeziehen, so wird zur linearen Näherung noch die zweite Ableitung hinzugefügt. Die Näherungsfunktion wird dadurch etwas aussagekräftiger. Die zweite Ableitung wird mit dem Faktor 2 im Nenner gewichtet.
T2(x) = f(xo) + f'(xo).(x – xo) + f“(xo).(x – xo)²/2 ist eine quadratische Näherungsfunktion für f(x) an der Stelle xo=a.
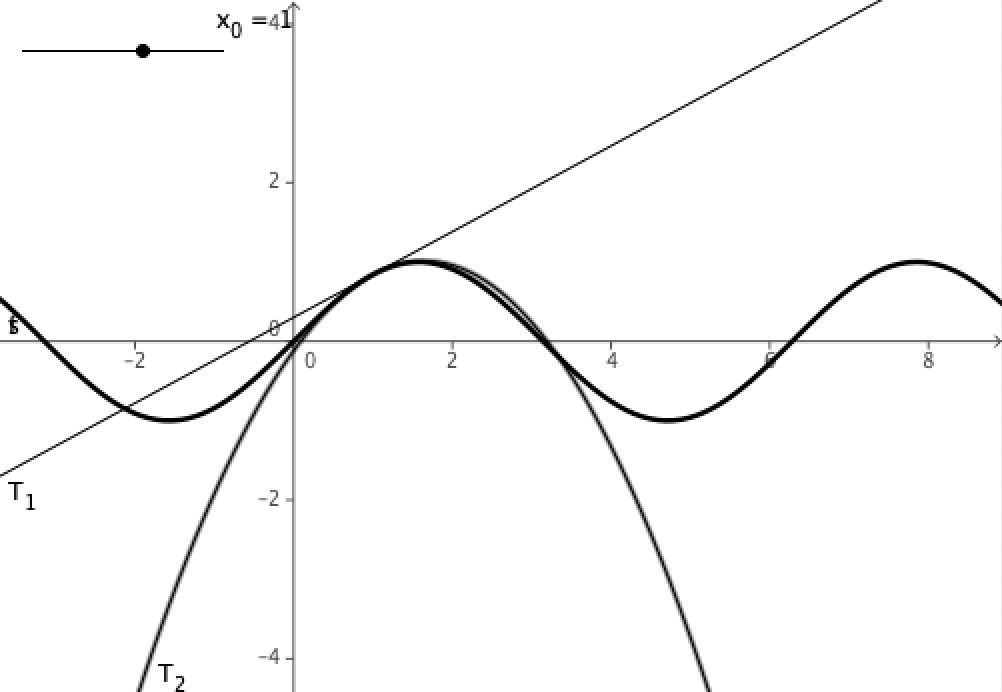
Zur Systematik dieser Entwicklung
Die erste Ableitung wird mit dem Term (x – a) bzw. (x – xo) multipliziert.
Die zweite Ableitung wird mit dem Term (x – a)² bzw. (x – xo)² multipliziert.
Der Faktor (x – a) bedeutet, dass der Fehler der Näherung größer wird, je weiter der x-Wert von a entfernt ist. Bei x = a bleibt als Näherung genau der Funktionswert übrig. Man nennt a den Entwicklungspunkt der Taylorreihe. Der Entwicklungspunkt ist jener Punkt, in dessen Umgebung das Verhalten der Funktion sinnvoll angenähert wird. Je höher die Ableitung, umso stärker wird aufgrund der Potenz von (x – a) der Fehler wenn | x – a | > 1.
Jede Ableitung wird mit einem Faktor im Nenner gewichtet, der angibt, wie stark die jeweilige Ableitung in der Näherungsfunktion berücksichtigt wird. Die Gewichtung der n-ten Ableitung ist n!, die Gewichtung der einzelnen Ableitungen hängt mit den höheren Ableitungen der Potenzfunktion zusammen und soll hier nicht näher erklärt werden.
Je mehr Ableitungen in der Taylor-Entwicklung gebildet werden, desto genauer wird die Funktion f durch die Taylor-Entwicklung (oder Taylor-Reihe) angenähert.(T17 hellgrün)
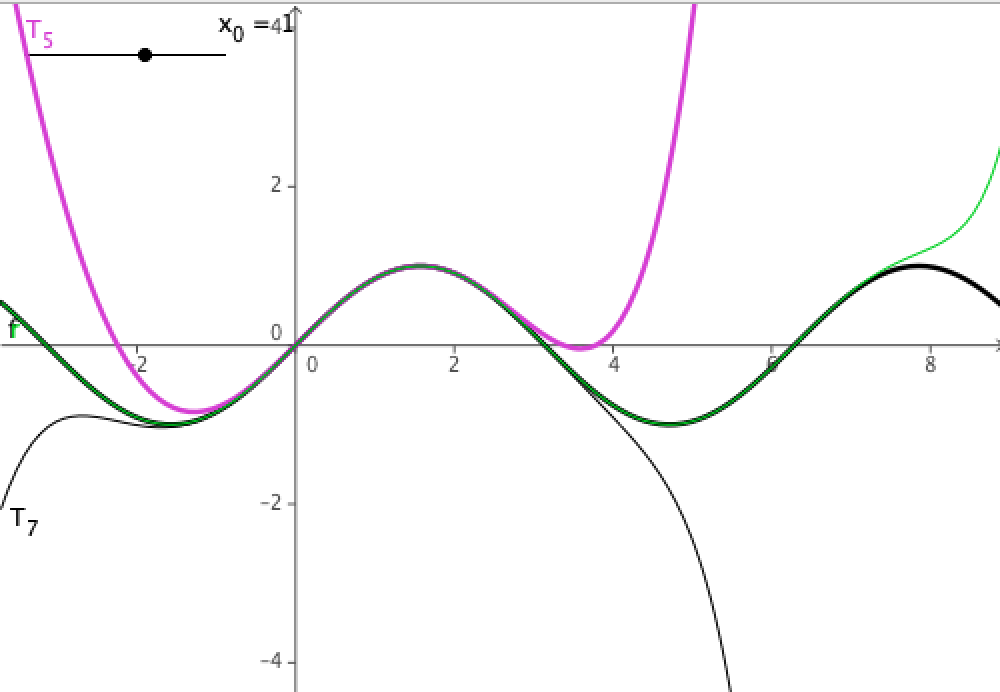
Die Taylor-Reihe entspricht der Funktion, wenn unendlich viele Ableitungen summiert werden.
Visualisierung
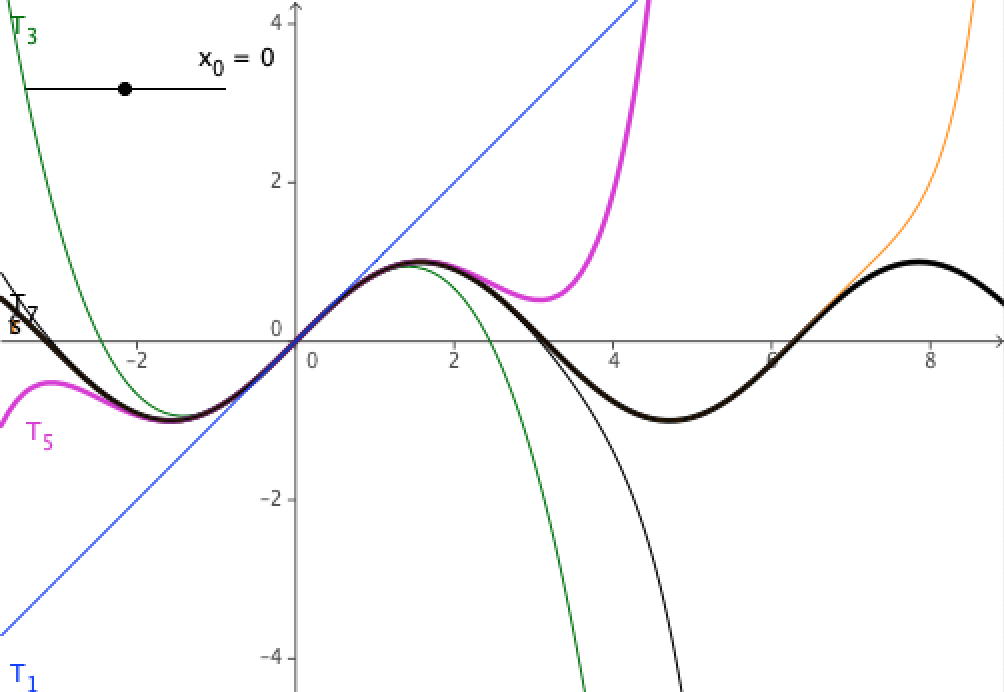
Die Grafik zeigt mehrere Taylor-Polynome für f(x) = sin(x) am Entwicklungspunkt a = 0. Die blaue Gerade ist die erste Näherung T1(x), die grüne Funktion die kubische Näherung T3(x), etc. In der Umgebung des Entwicklungspunktes ist die Abweichung von sin(x) bereits sehr klein.
Allgemein ist eine Funktion f auch als n-tes Taylorpolynom der Funktion f mit einem Fehler (Restglied-Polynom) darstellbar.
Die Differenz zwischen Näherung und Funktion lässt sich mit Hilfe von Restglied-Polynomen Rn(x) ausdrücken. Man kann Aussagen über das Restglied-Polynom machen, das übersteigt aber bei Weitem die Mathematik der höheren Schule. Jedenfalls ist der Fehler größer, je stärker x vom Entwicklungspunkt a abweicht.
Für den Spezialfall a = 0 nennt man die Taylor-Polynome MacLaurin-Polynome oder MacLaurin-Reihe. Die MacLaurin-Reihe hat gegenüber dem allgemeinen Term der Taylor-Reihe den Vorteil des einfacheren Funktionsterms.
Wichtige Taylor- bzw. MacLaurin-Polynome
Bemerkenswert sind die MacLaurin-Reihen für folgende Funktionen:
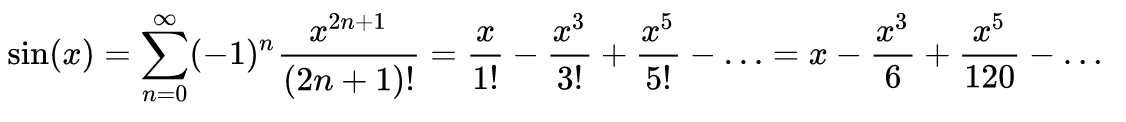
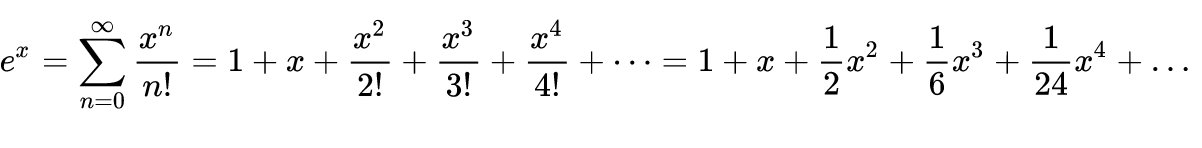
Setzt man x = 1 in der MacLaurin-Reihe von ex, so erhält man für den Wert der Zahl e die Reihe
e = 1 + 1 +1/2! + 1/3! + …
Beachte den Zusammenhang zwischen den Polynomen für sin(x) und cos(x)!
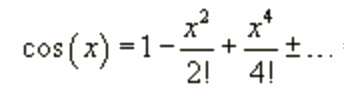


 2. Platz für eContent für eLearning in der Kategorie Sekundarstufe II am 10.11.2014 in Wien gemeinsam mit Mag. Hannes Mitterlehner (Mitte) für das Projekt
2. Platz für eContent für eLearning in der Kategorie Sekundarstufe II am 10.11.2014 in Wien gemeinsam mit Mag. Hannes Mitterlehner (Mitte) für das Projekt 