Taylorpolynome: Simulation 1
gedruckt am 01. Mar. 2026
Folgendes dynamische Arbeitsblatt (geogebra) zeigt, wie sich die ersten Taylor-Polynome als Näherungsfunktion für eine Funktion am Entwicklungspunkt entwickeln, wenn man den Entwicklungspunkt verschiebt.
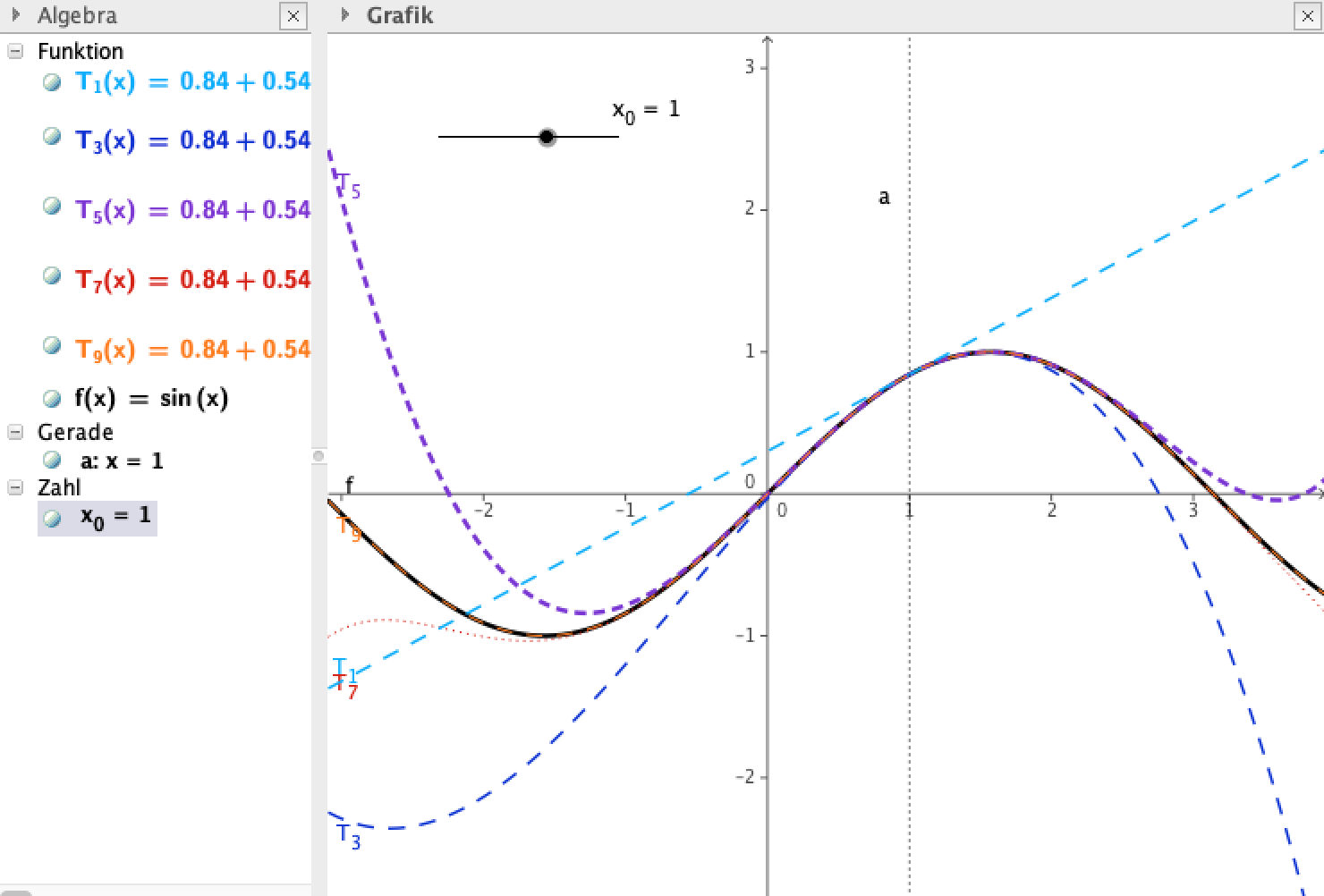
Die Grafik zeigt die 1., 3., 5., 7. und 9. Näherungsfunktion am Entwicklungspunkt 1.
Die Funktion ist f(x) = sin(x). T1(x) gibt die erste Näherung an (hellblau), sie ist die Tangente am Entwicklungspunkt. T3(x) ist eine kubische Funktion (dunkelblau). Mit jedem weitere Taylorglied wird die Funktion f(x) in einem bestimmten Intervall um den Entwicklungspunkt besser angenähert. In der Abbildung oben kann man beobachten, dass T5(x) die Funktion sin(x) (pink strichliert) im Intervall (-0.5 | 2.5) recht gut annähert, T7(x) (rot punktiert) im Intervall (-1.5 | 3.3) und T9(x) (orange, auf f(x)) bereits im gesamten dargestellten Bereich.
Der Entwicklungspunkt kann mit dem Schieberegler im Geogebra-Applet verschoben werden, die punktierte senkrechte Linie zeigt in der Grafik die Lage des Entwicklungspunktes an. In einem Intervall um diesen Entwicklungspunkt ist die Näherung halbwegs genau – je nachdem, wie groß das Intervall ist und wie viele Reihenglieder das Taylor-Polynom hat.
Arbeitsblatt Geogebra
Erstellt mit GeoGebra
Die Systematik dieser Taylor-Entwicklungen stelle ich im Beitrag https://www.jomo.org/index.php/taylorreihen-und-taylorpolynome dar.
Arbeitsanleitungen
- Verfolge grafisch die Näherungsfunktionen für f(x) bei Verschiebung des Entwicklungspunktes mit dem Schieberegler!
- Überprüfe (durch Nachrechnen) die jeweiligen Funktionsterme der Taylorpolynom je nach Wahl des Entwicklungspunktes!
- Mit einem Doppelklick auf den Funktionsterm links kannst du einen anderen Funktionsterm eingeben und die Analyse mit anderen Funktionen durchführen: beispielsweise mit f(x) = sin(x). Die richtigen Taylorpolynome werden automatisch berechnet.


 2. Platz für eContent für eLearning in der Kategorie Sekundarstufe II am 10.11.2014 in Wien gemeinsam mit Mag. Hannes Mitterlehner (Mitte) für das Projekt
2. Platz für eContent für eLearning in der Kategorie Sekundarstufe II am 10.11.2014 in Wien gemeinsam mit Mag. Hannes Mitterlehner (Mitte) für das Projekt 