Drehung von Figuren im Koordinatensystem – Drehmatrizen
gedruckt am 03. Mar. 2026
Thema
- Löse das Problem mit Hilfe einer genauen Zeichnung graphisch!
- Überlege anhand deiner Zeichnung, wie dieses Problem mit Hilfe von Winkelfunktionen auch rechnerisch gelöst werden kann!
- Versuche, diese Problemlösung für beliebige Punkte und Winkel zu verallgemeinern!
- Erfinde weitere Aufgaben mit Figuren, die gedreht werden!
- Erstelle ein Arbeitsblatt in EXCEL, das die Aufgabe der Drehung einer Figur bei Eingabe eines Drehwinkels simuliert!
Anleitung
Das Problem kann mit Hilfe der Polarkoordinaten oder mit Hilfe von Drehmatrizen gelöst werden.
Polarkoordinaten
Die Ausgangspunkte werden in Polarkoordinatenform (a1,r) verwandelt, zum Winkel a1 wird der Winkel a addiert. Die Koordinaten des so gedrehten Punktes werden in rechtwinkelige Koordinaten verwandelt. Diese Variante ist unmittelbar einsichtig und bedarf keiner Kenntnis von (Dreh-)Matrizen. Allerdings sind Kenntnisse der komplexen Zahlen und der Winkelfunktionen nötig.
Drehmatrix
Ein Punkt (als Teil einer Figur) kann auch mit Hilfe von Matrizenmultiplikation gedreht werden. Die entsprechende Matrix heißt Drehmatrix (Drehwinkel a).
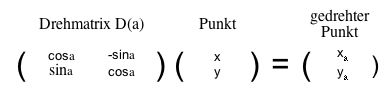
Abb. 1
Die Äquivalenz mit der Berechnung mit Hilfe der Polarkoordinaten wird durch die Additionstheoreme der Winkelfunktionen gezeigt:
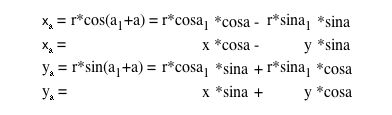
Abb. 2
Wie kommt man eigentlich zur Drehmatrix? Ganz einfach: Aus den Gleichungen für die x- und y-Koordinaten der letzten Umformung kann die Drehmatrix entnommen werden.
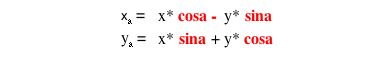
Abb. 3
xls: Drehung mit Polarkoordinaten und Matrizen
Verallgemeinerung und weitere Fragestellungen für Spezialisten
- Ergänze die Drehung mit einem Streckungsfaktor zu einer Drehstreckung!
- Erweitere die Drehung für einen beliebigen Drehpunkt im Koordinatensystem!
- Ergänze Drehung und Streckung mit der Spiegelung um die x- oder y-Achse!
- Erweitere die Spiegelung um parallele Gerade zu den Achsen als Spiegelungsachsen!
- Erweitere das Modell der Spiegelung um beliebige Geraden als Spiegelungsachsen!


 2. Platz für eContent für eLearning in der Kategorie Sekundarstufe II am 10.11.2014 in Wien gemeinsam mit Mag. Hannes Mitterlehner (Mitte) für das Projekt
2. Platz für eContent für eLearning in der Kategorie Sekundarstufe II am 10.11.2014 in Wien gemeinsam mit Mag. Hannes Mitterlehner (Mitte) für das Projekt 