jomo.org

• Die Ableitung einer linearen Funktion ist eine konstante Funktion (da die Steigung einer linearen Funktion konstant ist).
• Die Ableitung einer quadratischen Funktion ist eine lineare Funktion.
• Die Ableitung einer kubischen Funktion ist eine quadratische Funktion.
• Die Ableitung einer beliebigen Potenzfunktion ist eine Potenzfunktion.
• Die Ableitung einer (einfachen) Winkelfunktion ist eine Winkelfunktion (ausgenommen Tangens).
• Die Ableitung einer Exponentialfunktion ist eine Exponentialfunktion.

Wir können diese Zusammenhänge zwischen den Funktionstermen ohne Grenzwertrechnung zwar (noch) nicht rechnerisch ermitteln, aber zumindest grafisch nachvollziehen. Bei den Funktionstermen wird ein klarer und einfacher Zusammenhang zwischen Funktion und Ableitung sichtbar.

Zusammenhang zwischen den Funktionstermen und den beiden Funktionsgraphen: Polynomfunktion 3. Grades

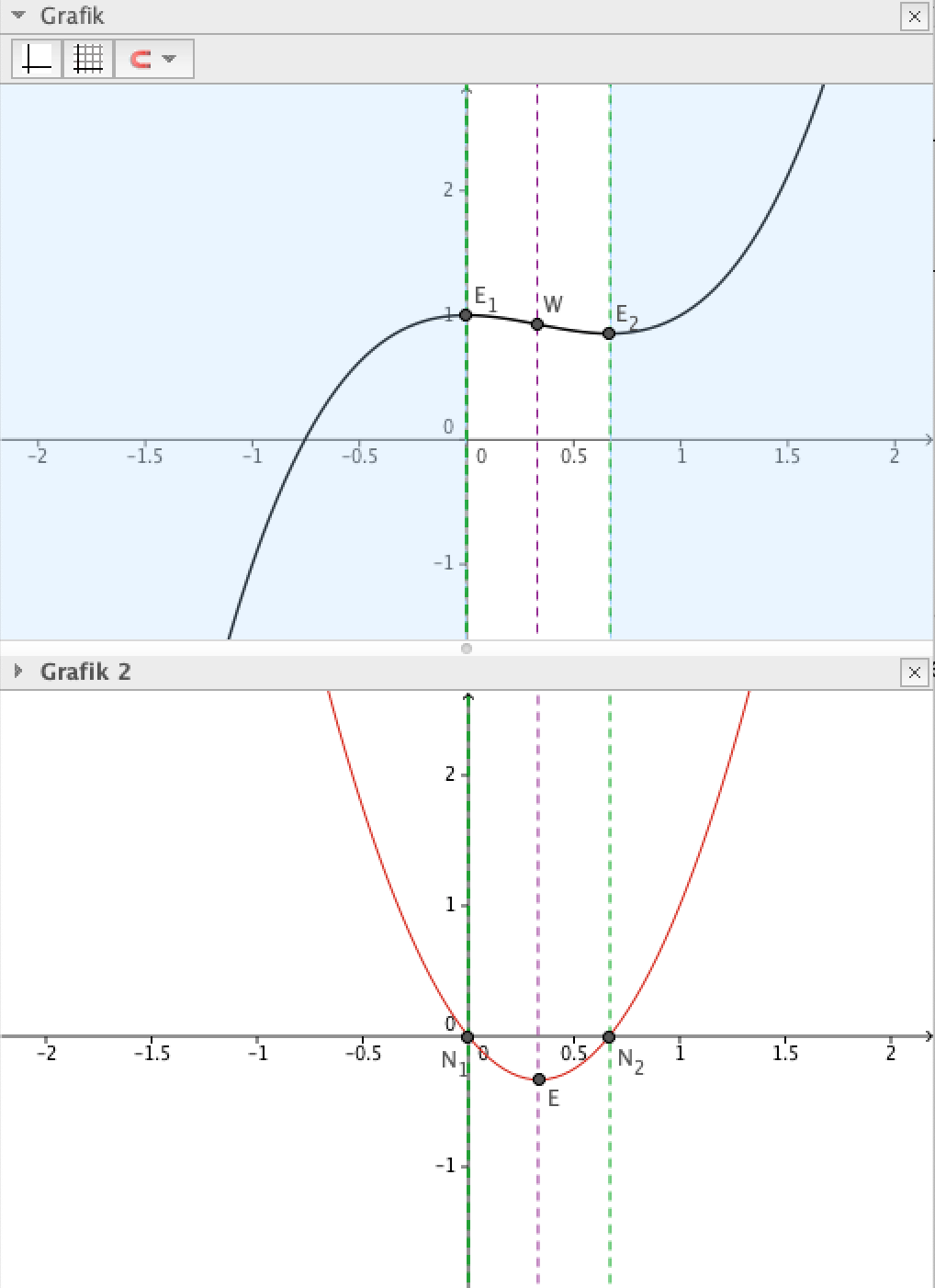
Abbildung: kubische Funktion und Ableitung

f(x) = x³ – x² + 1 (schwarz, oben) und f´(x)= 3x² -2x (rot, unten)
Die Ableitung dieser kubischen Funktion ist eine quadratische Funktion, die Funktionsterme hängen auf einfache Weise zusammen.

• Im Intervall x<0 (linker hellgrauer Bereich) sind die Tangentensteigungen positiv, daher die y-Werte der Ableitung positiv.
• Im Bereich x>0.67 (rechter hellgrauer Bereich) sind die Tangentensteigungen positiv, daher die y-Werte der Ableitung positiv.
• Im Bereich dazwischen ist f(x) fallend, daher sind die y-Werte der Ableitung negativ.
• Der Wechsel geschieht an den Extremstellen von f(x) E_1 und E_2 (grün strichliert). Das entspricht den Nullstellen von f‘.
• Der stärkste negative Wert ist beim Extremum E der Ableitung, das entspricht dem Wendepunkt W von f(x).
• Aus diesen grafisch sichtbaren Zusammenhängen ergibt sich auch, wie man diese markanten Punkte (Extrema, Wendepunkte) berechnet: Für die Extrema von f berechnet man die Nullstellen von f‘, für den Wendepunkt die Extrema von f‘ (das sind dann die Nullstellen vonf“).

Zusammenhang zwischen den Funktionstermen und den beiden Funktionsgraphen: Winkelfunktion

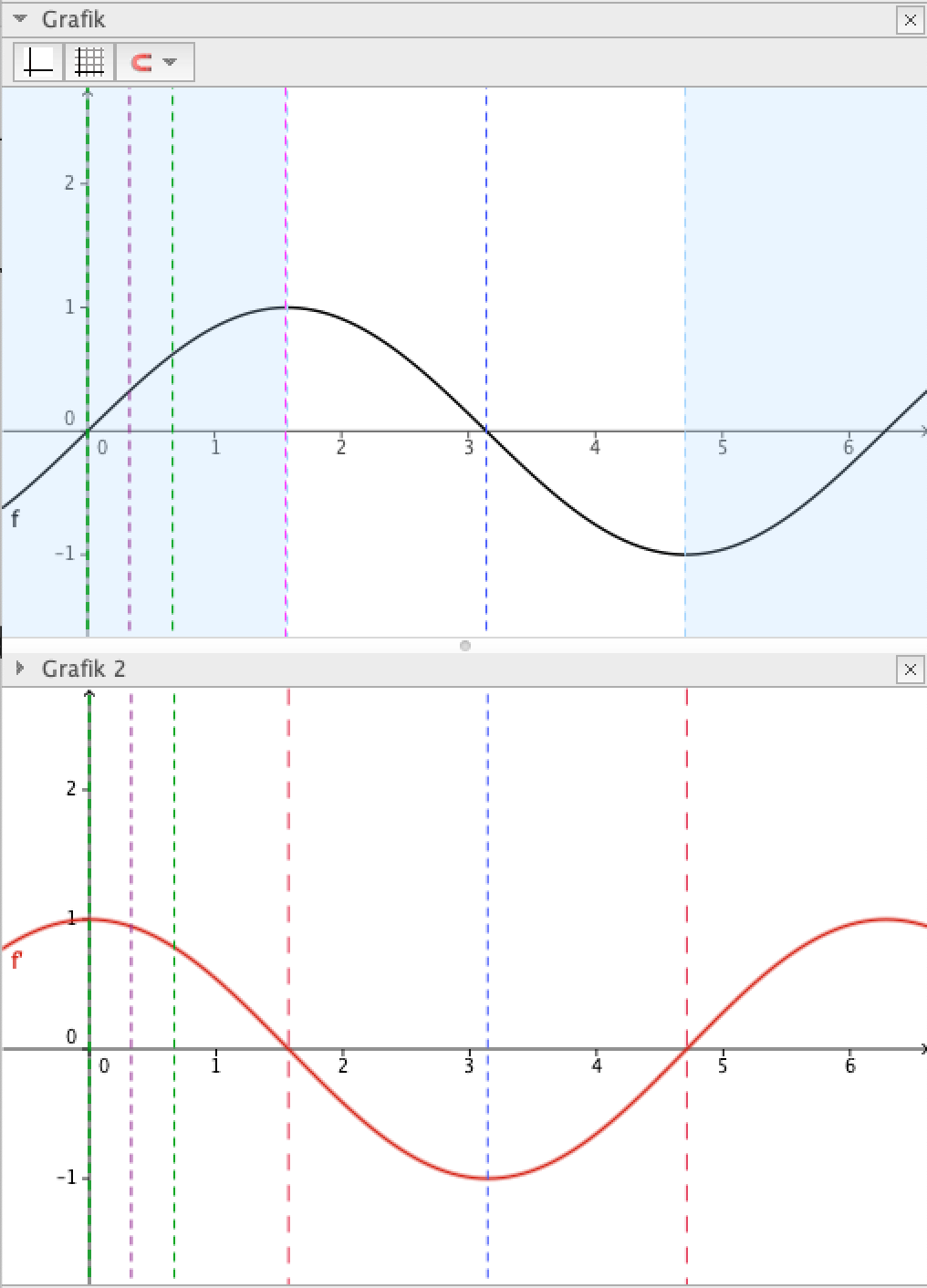
Skizze: Winkelfunktion und Ableitung

Beobachte wie oben die Zusammenhänge zwischen den Funktionstermen und Funktionsgraphen.

Zusammenhang zwischen den Funktionstermen und den beiden Funktionsgraphen: Exponentialfunktion

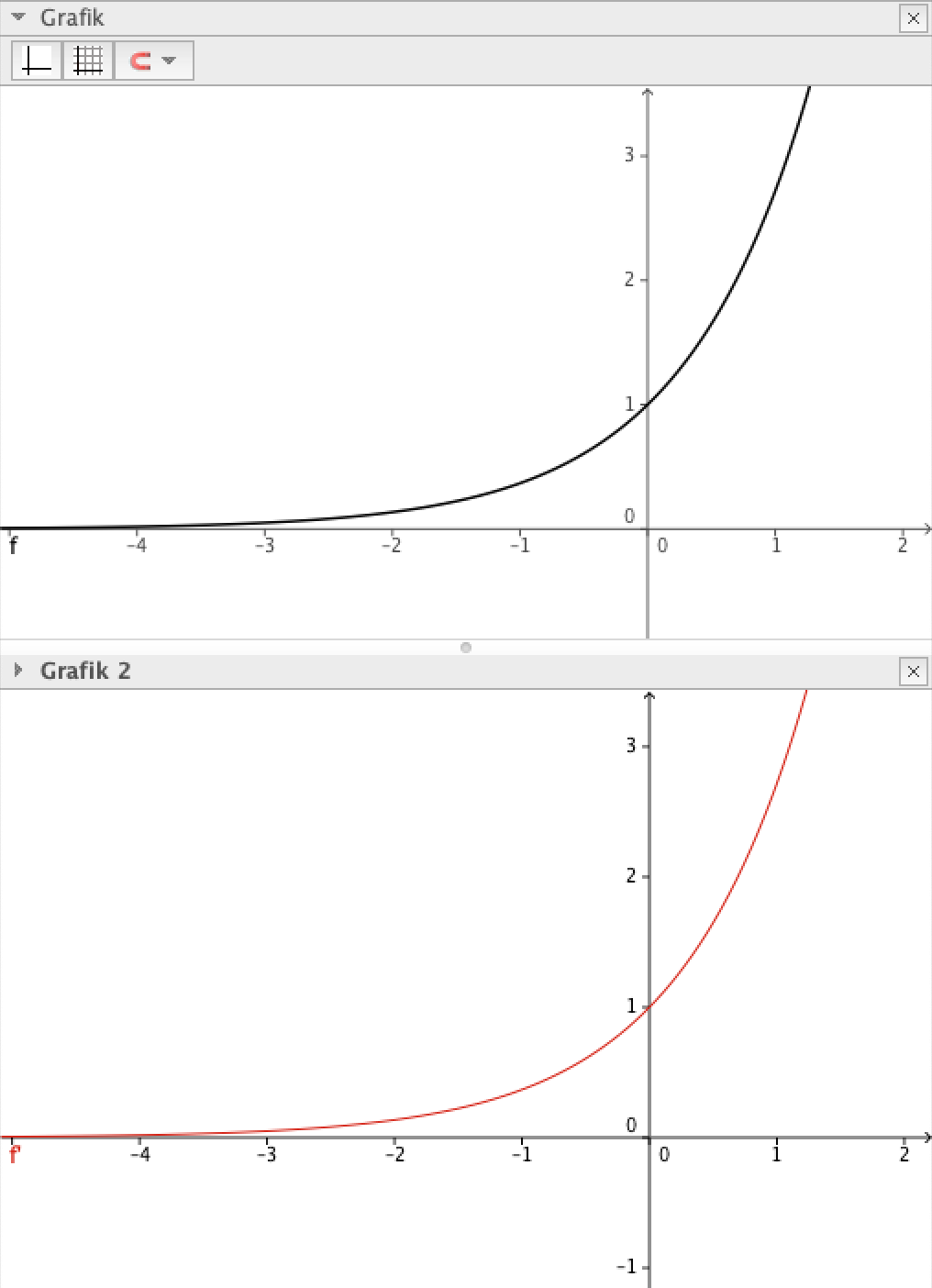
Skizze: Exponentialfunktion und Ableitung

Beobachte wie oben die Zusammenhänge zwischen den Funktionstermen und Funktionsgraphen.

• Die Funktion f ist überall monoton steigend.
• Die Steigung (y-Wert der Ableitung) bei x=0 ist 1.
• Die Funktion f steigt für größere x immer stärker, daher werden die y-Werte der Ableitung immer größer.

Es bestehen u.a. folgende Zusammenhänge

f(x) = kx+d, dann ist f'(x) = k (das ist ja die Steigung der Geraden)
f(x) = sin(x), dann ist f'(x) = cos(x)
f(x) = cos(x), dann ist f'(x) = sin(x)
f(x) = exp(x), dann ist f'(x) = exp(x)