Experimentelle Integralrechnung: Flächen
gedruckt am 02. Jan. 2026
Thematische Voraussetzung ist die Differentialrechnung. Die Erinnerung an zwei Zusammenhänge halte ich hier für wesentlich:
- Die y-Werte der ersten Ableitung einer Funktion f(x) repräsentieren die Tangentensteigungen dieser Funktion f(x) an den jeweiligen x-Werten.
- Die Funktionsterme von f(x) und ihrer ersten Ableitung f'(x) hängen miteinander zusammen.
Flächenberechnungen
Wir experimentieren mit Flächenberechnungen und verwenden dazu Geogebra. Geogebra ist gratis, einfach zu bedienen und hat eine unglaubliche Funktionalität, die den experimentellen Zugang zu Mathematik hervorragend unterstützt.
Experiment 1
Wir definieren eine Funktion f(x) = x und betrachten die Fläche zwischen x-Achse und Funktion zwischen x=0 und x=1. Geogebra berechnet und kennzeichnet diese Fläche mit dem Befehl INTEGRAL[f(x),0,1]. Das Ergebnis ist klarerweise 1*1/2 = 1/2, das halbe Quadrat 1*1.
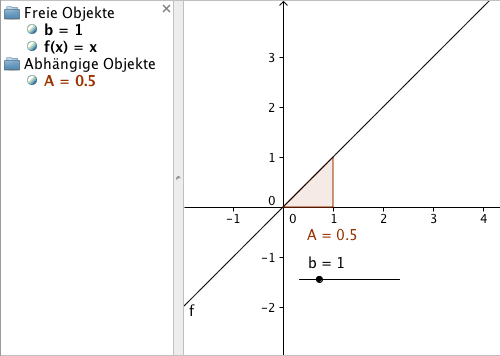
Die Fläche von x=0 bis x=2 – INTEGRAL[f(x),0,2] – ergibt 2*2/2 = 2.
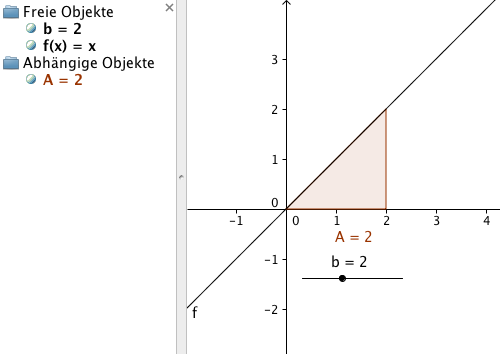
Für weitere Flächen ergibt sich aus der Formal x*x/2 bzw. x2/2 wiederum jeweils ein halbes Quadrat.
Es sei hier auf einen besonderen Zusammenhang hingewiesen: f(x) = x ist die Ableitung der Funktion F(x) = x2/2, und das ist die Flächenberechnungsformel für die Fläche zwischen f(x) und x-Achse. Wir werden mit Hilfe einer anderen (vorerst linearen) Funktion testen, ob dieser Zusammenhang zwischen Funktion und Flächenformel auch bei anderen Funktionen gilt.
Experiment 2
Berechnen wir die Flächen zwischen f(x) = 2x und x-Achse von Null weg. Als Formel für den Flächeninhalt erhalten wir A = 2x2/2 = x2. Von F(x) = x2 ist f(x) = 2x die Ableitung. Dieser Zusammenhang ist bei allen linearen Funktionen festzustellen.
Wie bei der Differentialrechnung die Tangentensteigung an einer Stelle x als y-Wert aufgetragen wurde, trage ich hier den Flächeninhalt bis b an der Stelle x=b als y-Wert auf. Beachten Sie zuerst, was der y-Wert von PA bedeutet und verändern Sie den Schieberegler-Wert von b : Die Spur des Punkte PA zeigt den Funktionsverlauf von F(x).
Mit Doppelklick auf die Funktion f(x)=2x können Sie den Funktionsterm verändern. Als Kommazeichen verwenden Sie den Punkt!
Verallgemeinerung
Tatsächlich gilt dieser Zusammenhang auch für nicht-lineare Funktionen.
Zusammengefasst lässt sich folgendes sagen:
- Es ist möglich, die Fläche zwischen einer (nicht-linearen) Funktion f(x) und x-Achse zu berechnen. Die Formel für den Flächeninhalt hängt mit dem Term jener Funktion F(x) zusammen, von der die Ableitung f(x) ist. Das ist ein bemerkenswerter Zusammenhang! Warum das so ist, wird in einem eigenen Beitrag geklärt.
- Der Flächeninhalt kann in beliebigen Intervallen (a,b) berechnet werden. Der Flächeninhalt ist durch F(b) – F(a) bestimmt, wobei F(x) jene Funktion ist, von der f(x) die Ableitung ist. Achtung: Liegt im Intervall eine Nullstelle, muss der Flächeninhalt abschnittweise berechnet werden. Warum das so ist, wird in einem eigenen Beitrag geklärt.
Bei Kenntnis von Ableitungen können die Flächeninhalte zwischen Ableitung F'(x)=f(x) und x-Achse manuell nachgerechnet werden.
Beispiel
Wir berechnen die Flächen zwischen f(x) = x2 und x-Achse von x = 0 bis 1, 2, 3 bzw. von 1 bis 3 und überprüfen, ob auch der Zusammenhang zwischen Flächenformel und erster Ableitung besteht.
Nachdem f(x) = x2 die Ableitung von F(x) = x3/3 ist (Gegenprobe: Ableitung bilden!) ergibt sich für die gesuchten Flächeninhalte:
(0,1): F(1) – F(0) = 1/3
(0,2): F(2) – F(0) = 8/3 = 2,67
(0,3): F(3) – F(0) = 27/3 = 9
(1,3): F(3) – F(1) = 27/3 – 1/3 = 26/3 = 8,67
Auf Integrationsmethoden wird hier vorläufig verzichtet. Erstens gibt es genug Darstellungen in den klassischen Lehrbüchern und zweitens heißt es im Lehrplan der Handelsakademien „Einführung in die Integralrechnung“.


 2. Platz für eContent für eLearning in der Kategorie Sekundarstufe II am 10.11.2014 in Wien gemeinsam mit Mag. Hannes Mitterlehner (Mitte) für das Projekt
2. Platz für eContent für eLearning in der Kategorie Sekundarstufe II am 10.11.2014 in Wien gemeinsam mit Mag. Hannes Mitterlehner (Mitte) für das Projekt 