Uneigentliche Integrale und die Asymptote der Integralfunktion
gedruckt am 02. Jan. 2026
Uneigentliche Integrale sind bestimmte Integrale (Flächeninhalte), die auf einer Seite nicht begrenzt sind und trotzdem einen endlichen Flächeninhalt haben. Die Berechnung dieser uneigentlichen Integrale geschieht über die Grenzwert-Rechnung.
Wir betrachten die Funktion f(x) = 1/x2 (schwarz). Von dieser Funktion bilden wir eine Stammfunktion (rot):
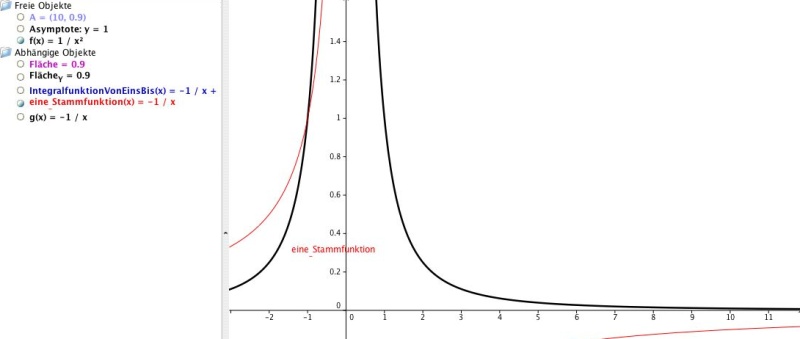
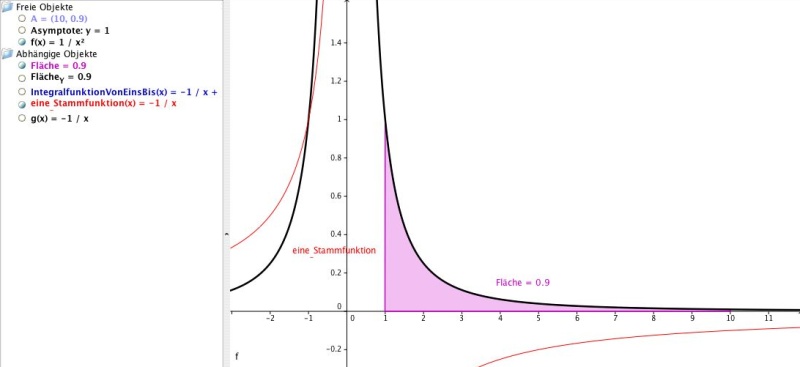
Wir berechnen den Flächeninhalt (pink) zwischen Funktion f(x) und x-Achse im Intervall [1, 10]. Dieser Flächeninhalt beträgt 0.9 Einheiten. Wählt man jetzt eine größere obere Grenze, wird der Flächeninhalt etwas größer. Wie groß man die obere Grenze des Intervalls auch wählt, der Flächeninhalt wird nie 1 erreichen. Der Wert 1 ist der Grenzwert, weil 1 die kleinstmögliche Zahl ist, durch die der Flächeninhalt begrenzt ist. So ein bestimmtes Integral mit unendlich großer oberer Grenze nennt man uneigentliches Integral, wenn ein Grenzwert existiert.
Ich bilde die Integralfunktion G(x) (blau), das ist jene Stammfunktion mit dem Funktionsterm F(x) – F(a). Die Funktionswerte dieser Integralfunktion G(x) geben genau die Größe des Flächeninhalts von a (untere Intervall-Grenze) bis zum jeweiligen x-Wert an.
Als (eine beliebige) Stammfunktion erhalten wir F(x) = -1/x.
In unserem Fall ist dann G(x) = F(x) – F(1) = -1/x – (-1/1),
also G(x) = -1/x + 1.
Wir überprüfen in der Zeichnung:
- G(1) muss Null sein, weil 1 die untere Grenze ist und von 1 bis 1 noch keine Fläche entsteht. Die Integralfunktion G(x) hat in x = a (hier a=1) eine Nullstelle.
- G(x) wächst mit fortschreitendem x zuerst schneller, dann langsamer, weil die Fläche (pink) zuerst größer und dann kleiner ist.
- Der Funktionswert G(10) = 0.9, weil der Flächeninhalt zwischen f(x) und x-Achse von [1,10] den Wert 0.9 hat.
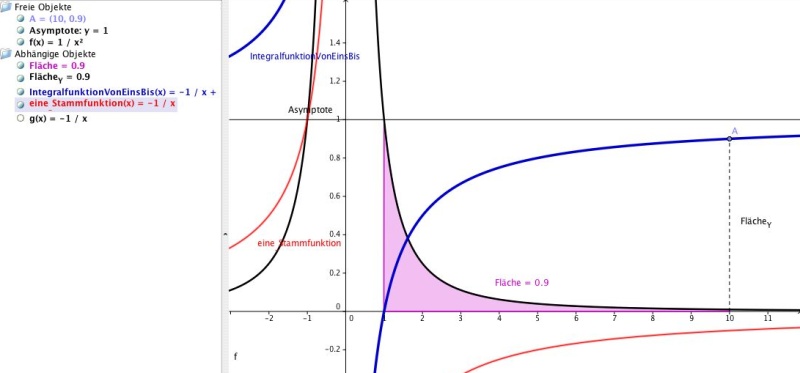
Jetzt kommt noch die Asymptote als Erklärungsmodell für die Begrenzung des Flächeninhalts für unendlich große Intervallgrenze b dazu: Die Asymptote der Funktion G(x) ist die zur x-Achse parallele Gerade y = 1. Das kannst du durch Polynom-Division berechnen, das geht aber auch aus der Grafik klar hervor: Die Funktionswerte von G(x) werden nie größer als 1. Und weil die y-Werte von G(x) die Flächeninhalte unter f(x) von 1 weg repräsentieren, sind auch diese nie größer als 1!
Als einfache grafische Überprüfung, ob eine Funktion f(x) ein uneigentliches Integral hat, genügt es zeigen, ob die Stammfunktion eine horizontale Asymptote hat. Die Höhe der Asymptote der Integralfunktion ist dann gleichzeitig der Wert des uneigentlichen Integrals. Uneigentlich heißt das Integral deshalb, weil man im klassischen Sinne eigentlich nicht von einem Flächeninhalt sprechen kann, wenn die Fläche nach einer Seite offen ist.


 2. Platz für eContent für eLearning in der Kategorie Sekundarstufe II am 10.11.2014 in Wien gemeinsam mit Mag. Hannes Mitterlehner (Mitte) für das Projekt
2. Platz für eContent für eLearning in der Kategorie Sekundarstufe II am 10.11.2014 in Wien gemeinsam mit Mag. Hannes Mitterlehner (Mitte) für das Projekt 